Elektřina a magnetismus

Nestacionární magnetické pole

Elektromagnetická indukce

Při změně magnetického pole v okolí cívky vzniká v cívce indukovaný elektrický proud

Stacionární (zřídlové) el. pole

Nestacionární (vírové) el. pole má siločáry uzavřené křivky

Magnetický indukční tok

= Charakteristická veličina nestacionárního mag. pole

Značka: Φ\Phi

Definiční vztah:

Φ=B⋅S⋅cos⁡(α)\Phi = B \cdot S \cdot \cos(\alpha)

BB ... magnetická indukce

SS ... plocha závitu

α\alpha ... úhel mezi normálou plochy závitu a MIČ (magnetickými indukčními čarami)

Jednotkou mag. indukčního toku je weber:

Φ=Wb\Phi = \text{Wb}

Faradayův zákon elektromagnetické indukce

Popisuje, jaká je změna Φ\Phi v čase

Vodič se pohybuje v magnetickém poli

Odvození vztahu pro indukované napětí:

Fe=FmE⋅e=B⋅e⋅vE=B⋅vUi=E⋅dUi=E⋅lUi=B⋅v⋅l\begin{align*} F_\text{e} &= F_\text{m} \\[0.5em] E \cdot e &= B \cdot e \cdot v \\[0.5em] E &= B \cdot v \\[1em] U_\text{i} &= E \cdot d \\[0.5em] U_\text{i} &= E \cdot l \\[0.5em] U_\text{i} &= B \cdot v \cdot l \end{align*}

UiU_\text{i} ... indukované napětí

ll ... aktivní délka vodiče

Δs=v⋅ΔtUi=B⋅ΔsΔt⋅lUi=B⋅ΔSΔtUi=−ΔΦΔt\begin{align*} \Delta s &= v \cdot \Delta t \\[0.5em] U_\text{i} &= B \cdot \frac{\Delta s}{\Delta t} \cdot l \\[1em] U_\text{i} &= B \cdot \frac{\Delta S}{\Delta t} \\[1em] U_\text{i} &= - \frac{\Delta \Phi}{\Delta t} \end{align*}

Indukované elektromotorické napětí je rovno záporné časové změně magnetického indukčního toku.

Vodič, který se pohybuje v magnetickém poli, se stává zdrojem indukovaného napětí s polaritou opačnou oproti klasickému zdroji

ΔΦ>0  ⟹  Ui<0ΔΦ<0  ⟹  Ui>0\begin{align*} \Delta \Phi > 0 \implies U_\text{i} < 0 \\[0.5em] \Delta \Phi < 0 \implies U_\text{i} > 0 \end{align*}

Rozdíl pohybu magnetu a nemagnetu vodivou trubkou: magnet se zpomalí

Přechodný děj a vlastní indukce cívky

Při zapnutí proudu se žárovka zapojená sériově s cívkou rozsvítí později, než žárovka zapojená s rezistorem

Při vypnutí žárovka s cívkou zhasne později, než žárovka s rezistorem

V cívce při zapnutí/vypnutí vzniká nestacionární magnetické pole →\to indukuje se proud – podle Lensova zákona: při sepnutí má indukovaný proud opačný směr než proud ze zdroje, při vypnutí má indukovaný proud stejný směr jako proud ze zdroje

Časový průběh proudu v obvodu s rezistorem:

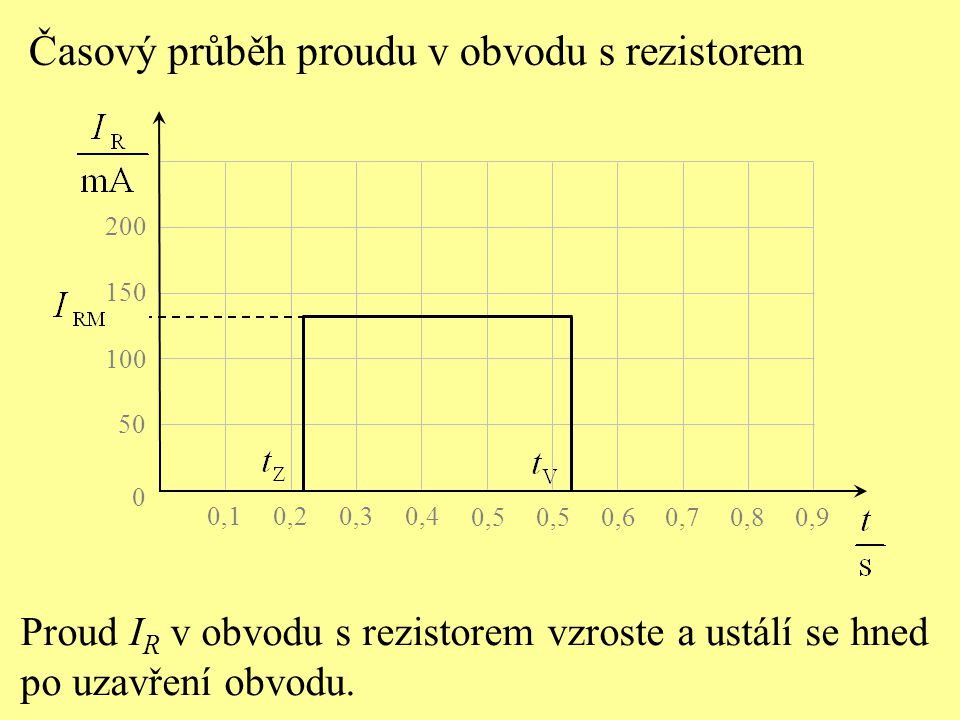
Časový průběh proudu v obvodu s rezistorem

Časový průběh proudu v obvodu s cívkou:

Časový průběh proudu v obvodu s cívkou

Napětí indukované na cívce:

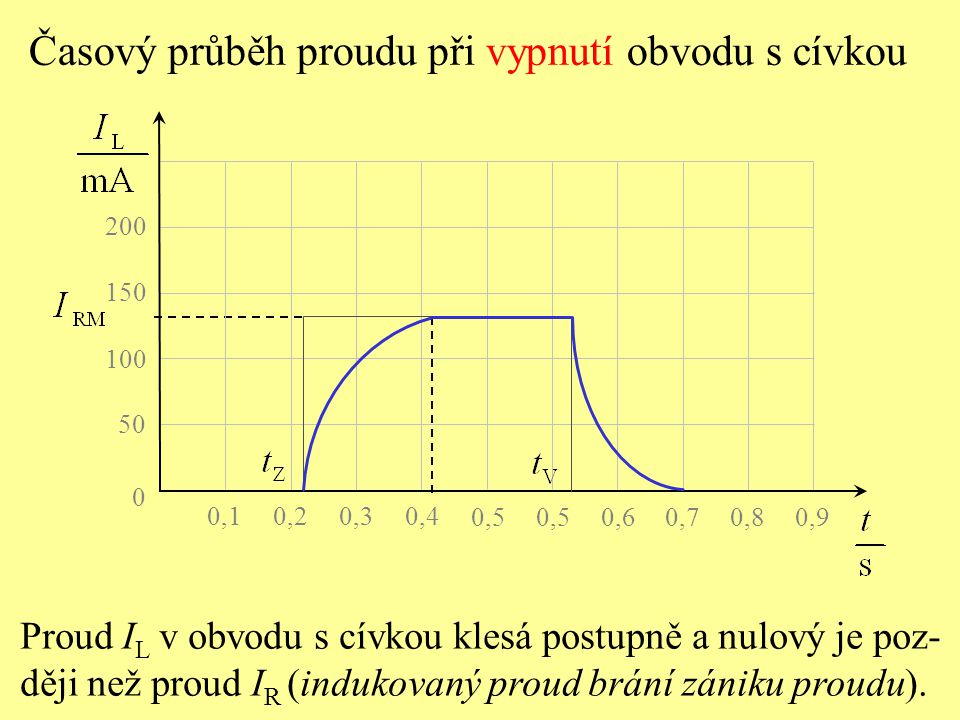
Napětí indukované na cívce

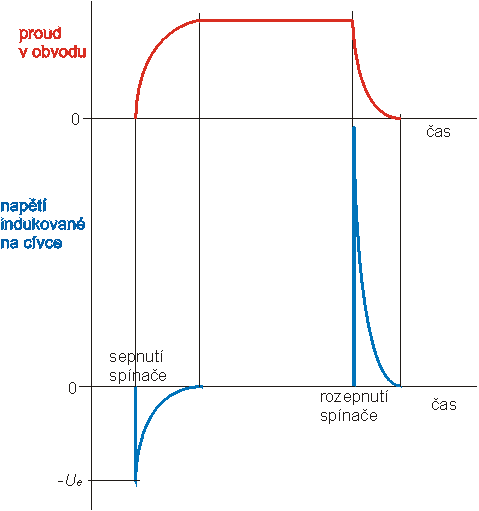
Změna magnetického indukčního toku je přímo úměrná změně elektrického proudu v cívce:

ΔΦ=k⋅ΔI\Delta \Phi = k \cdot \Delta I

Změna magnetického indukčního toku cívkou:

ΔB=μ0μr⋅N⋅ΔIlΔΦ=ΔB⋅N⋅S⋅cos⁡(α)ΔΦ=μ0μrN2SlΔIL=μ0μrN2SlΦ=L⋅I\begin{align*} \Delta B &= \mu_0 \mu_\text{r} \cdot \frac{N \cdot \Delta I}{l} \\[1em] \Delta \Phi &= \Delta B \cdot N \cdot S \cdot \cos(\alpha) \\[0.5em] \Delta \Phi &= \mu_0 \mu_\text{r} \frac{N^2 S}{l} \Delta I \\[1em] L &= \mu_0 \mu_\text{r} \frac{N^2 S}{l} \\[1em] \Phi &= L \cdot I \end{align*}

LL ... indukčnost cívky

Jednotkou indukčnosti je Henry:

[L]=H[L] = \text{H} \\[0.5em]

Podle Faradayova zákona:

a

Ui=−LΔIΔtU_\text{i} = - L \frac{\Delta I}{\Delta t}

Energie magnetického pole cívky

Energie zdroje se přemění na energii el. proudu v obvodu a na energii magnetického pole v okolí cívky (= platí zákon zachování energie):

Ez=Wz=Q⋅UeΔEm=L⋅I⋅ΔtΔEm=Φ⋅ΔI\begin{align*} E_\text{z} &= W_\text{z} = Q \cdot U_\text{e} \\[0.5em] \Delta E_\text{m} &= L \cdot I \cdot \Delta t \\[0.5em] \Delta E_\text{m} &= \Phi \cdot \Delta I \end{align*}

EzE_\text{z} ... energie zdrojea

EmE_\text{m} ... energie magnetického pole

Graf závislosti indukčního toku cívkou na proudu:

Graf závislosti indukčního toku cívkou na proudu

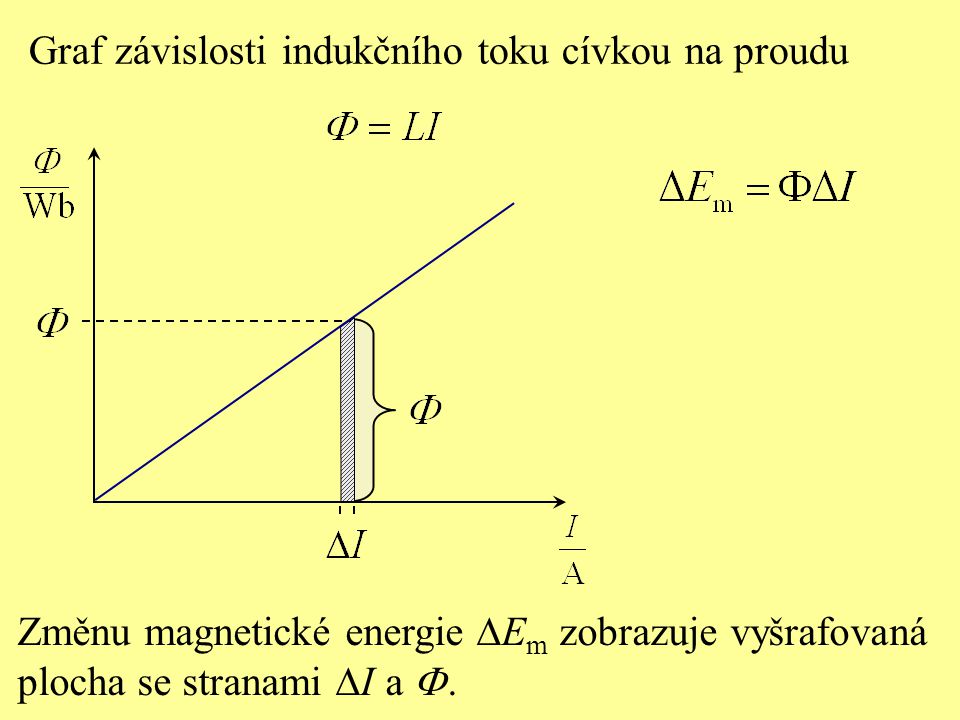
Výpočet energie magnetického pole z pracovního diagramu:

Em=12ΦIEm=12LI2\begin{align*} E_\text{m} &= \frac{1}{2} \Phi I \\[0.5em] E_\text{m} &= \frac{1}{2} L I^2 \end{align*}

→\to Indukčnost cívky (LL) charakterizuje setrvačnost elektrického obvodu