Speciální teorie relativity

V klasické fyzice je čas a hmotnost absolutní

Michelsonův experiment vyvrací teorii světelného éteru →\to žádná soustava není nadřazena jiné

Einsteinovy postuláty

  1. Princip relativity:

    Ve všech inerciálních vztažných soustavách platí stejné fyzikální zákony

    →\to Žádným experimentem provedeným uvnitř interciální vztažné soustavy nelze zjistit, zda se tato soustava vzhledem k jiné interciální vztažné soustavě pohybuje rovnoměrně přímočarým pohybem, nebo je v klidu

    = Rozšíření Galileova principu relativity

  2. Princip stálé rychlosti světla:

    Ve všech inerciálních vztažných soustavách má rychlost světla ve vakuu stejnou hodnotu (cc), a to nezávisle na pohybu světelného zdroje

Důsledky: Relativnost současnosti, dilatace času, kontrakce délek, relativistické skládání rychlostí, relativistická dynamika

Relativistické vztahy používáme pro v>13cv > \frac{1}{3} c

Relativnost současnosti

Různé nesoumístné události mohou být současné v jedné vztažné soustavě a nesoučasné v jiné

Dilatace času

V soustavě pohybující se rychlostí srovnatelné s rychlostí světla se čas prodlužuje

γ=11−v2c2t=γt0=t01−v2c2\begin{aligned} \gamma &= \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \\[1em] t &= \gamma t_0 = \frac{t_0}{\sqrt{1 - \frac{v^2}{c^2}}} \end{aligned}

γ\gamma ... Lorentzův koeficient

vv ... rychlost soustavy

Musí platit v<cv < c

Viz Paradox dvojčat

Kontrakce délek

Máme 2 soustavy SS a S′S'

Soustava S′S' se pohybuje vzhledem k soustavě SS rychlostí vv

V soustavě S′S' máme tyč délky l0l_0 rovnoběžnou s v⃗\vec{v}

Pozorovatel v soustavě SS naměří délku tyče ll

l=l0γ=l01−v2c2l = \frac{l_0}{\gamma} = l_0 \sqrt{1 - \frac{v^2}{c^2}}

Relativistické skládání rychlostí

Máme 2 soustavy SS a S′S'

Soustava S′S' se pohybuje vzhledem k soustavě SS rychlostí vv

V soustavě S′S' se pohybuje částice rychlostí u′u'

Pozorovatel v soustavě SS naměří rychlost částice uu

u=u′+v1+u′vc2u = \frac{u' + v}{1 + \frac{u'v}{c^2}}

Relativistická dynamika

Relativistická hmotnost

Při pohybu rychlosti v>13cv > \frac{1}{3} c se hmotnost tělesa zvětšuje

m=γm0m = \gamma m_0

m0m_0 ... klidová hmotnost

mm ... relativistická hmotnost (větší než klidová hmotnost)

Zákon zachování relativistické hmotnosti: Celková relativistická hmotnost izolované soustavy těles zůstává při všech dějích probíhajících v této soustavě konstantní

Relativistická hybnost

p⃗=mv⃗p⃗=γm0v⃗\begin{aligned} \vec{p} &= m \vec{v} \\[0.5em] \vec{p} &= \gamma m_0 \vec{v} \end{aligned}

Platí zákon zachování relativistické hybnosti

Relativistická energie

Změna hmotnosti soustavy je úměrná změně energie soustavy

ΔE=c2ΔmE=E0+Ek=konst.\begin{aligned} \Delta E &= c^2 \Delta m \\[0.5em] E &= E_0 + E_\text{k} = \text{konst.} \end{aligned}

E0E_0 ... klidová energie

Černé těleso

Černé těleso = těleso, které dokonale pohltí veškerou energii, která na něj dopadá

Černé těleso:

Černé těleso

Příklady černého tělesa z praxe: zornice, otevřené okno

Záření absolutně černého tělesa:

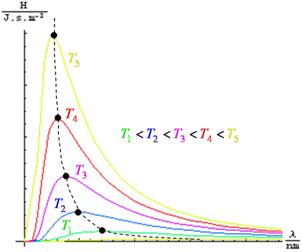
Záření absolutně černého tělesa

HH ... spektrální hustota intenzity vyzařování

H=f(λ,T)H = f(\lambda, T) \\[0.5em]

Wienův posunovací zákon:

λmax=bTb=2.9⋅10−3 m⋅K\begin{aligned} \lambda_\text{max} &= \frac{b}{T} \\[1em] b &= 2.9 \cdot 10^{-3} \ \text{m} \cdot \text{K} \end{aligned}

Stefan-Boltzmannův zákon:

Me=σ⋅T4σ=5.67⋅10−8 W⋅m−2⋅K−4\begin{aligned} M_e &= \sigma \cdot T^4 \\[0.5em] \sigma &= 5.67 \cdot 10^{-8} \ \text{W} \cdot \text{m}^{-2} \cdot \text{K}^{-4} \end{aligned}

σ\sigma ... Stefan-Boltzmannova konstanta

Funkce HH pro zmenšující se λ\lambda roste, ale skutečnost tomu neodpovídá (měla by klesat) →\to tzv. ultrafialová katastrofa

Max Planck říká, že energie je vyzařována po kvantech

E=h⋅fh=6.63⋅10−34 J⋅s\begin{aligned} E &= h \cdot f \\[0.5em] h &= 6.63 \cdot 10^{-34} \ \text{J} \cdot \text{s} \end{aligned}

hh ... Planckova konstanta

Spektra látky

Emisní spektrum = všechny vlnové délky světla, které těleso vyzařuje

Absorbční spektrum = všechny vlnové délky světla, které těleso pohlcuje

Rozžhavené molekuly vyzařují tzv. pásové spektrum

Spektrum každého prvku je jedinečné

Využití: spektroskopie – analýza složení materiálů

Chybějící zápis ze dní 28. 2. až 7. 3.

1927 – Davidson-Germerův experiment →\to elektrony mají vlnovou délku – potvrzení De Brogliovy teorie

E=U⋅e=12mv2b⋅sin⁡(α)=2k⋅λ2λ=hme⋅v\begin{aligned} E = U \cdot e &= \frac{1}{2} m v^2 \\[1em] b \cdot \sin(\alpha) &= 2k \cdot \frac{\lambda}{2} \\[1em] \lambda &= \frac{h}{m_e \cdot v} \end{aligned}

Druhá mocnina vlnové funkce určuje pravděpodobnost, že se částice nachází v daném okamžiku na daném místě

∣φ(x,y,z,t)∣2{\left| \varphi(x, y, z, t) \right|}^2

φ\varphi ... vlnová funkce

Nelze přesně určit polohu a rychlost částice – pracujeme pouze s pravděpodobnostmi

Emise záření

Např. LASER (= Light Amplification by Stimulated Emission of Radiation)

Využití: např. holografie